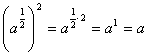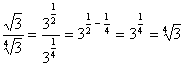Kvadratrøtter
Med ord:
Dersom a er et positivt tall, så er kvadratroten av a det positive tallet som multiplisert med seg selv blir a.
Med matematisk språkdrakt: Hvis
a ³
0, så er (
)2 = a.
Regneregler:
NB!! Det finnes ikke
tilsvarende regler for 
og 
!!
Bevis for multiplikasjonsregelen:
Vi
har at (
×
)2 = 
× 
× 
× 
= (
)2 × (
)2 = a × b
Þ 
×
= 
[NB: (
)2 er pr.
def. lik a × b ]
q.e.d. (latin: "quod e`rat demonstra`ndum" – oversatt: "hvilket skulle bevises")
Reglene ovenfor kan vi bruke til å skille ut kvadratiske faktorer.
Eksempel:
a) 
= 
b) 
Røtter av n-te grad
Vi tenker oss at vi har en terning med volum 2 og skal regne ut siden x.
Volum = x × x × x = x3 = 2
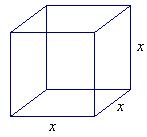
Vi skal altså finne et tall x som opphøyd i tredje
potens blir 2. Vi ser at 1 < x < 2, fordi 13 = 1 < 2
og 23 = 8 > 2. Det kan bevises at x blir et irrasjonalt
tall. Dette tallet skriver vi 
. (Dette er bare en skrivemåte noen har funnet på.)
Generelt: 
er et tall som
opphøyd i tredje potens gir a
Matematisk språk: (
)3 = a
Eksempel:
a) 
= 2 fordi 23 = 8
b) 
= -3 fordi (-3)3 = -27
Vi ser at vi kan beregne tredjerota av både positive og negative tall.
På tilsvarende måte definerer vi fjerderota (
), femterota (
), sjetterota (
) osv.
Generelt: Med 
(leses: "n-te
roten av a") mener vi det tallet som opphøyd i n-te potens
er lik a.
Potenser med brøkeksponenter
Vi er vant til å regne med potensuttrykk med heltallige
eksponenter – slik som 23, 52 og a5.
Men hva skal vi forstå med 
?
Vi forutsetter at a > 0. Vi ønsker at reglene for potensregning fortsatt skal gjelde.
En av disse reglene er følgende: (am)n = am × n
Bruker vi denne regelen på 
opphøyd i andre
potens, får vi:
oppfører seg altså akkurat lik
kvadratroten av 2. Vi definerer derfor 
som 
.
På samme måte definerer vi 
som 
.
Generelt: 
= 
når n Î N
Generelt definerer vi: 
når a > 0 og
t Î
N og n Î N
Opprettet 26.11.01
Høgskolen i Stavanger