Oppgave 6.6.43
På katetene og hypotenusen i en rettvinklet trekant er det tegnet halvsirkler. Vi skal regne ut arealet til det skraverte
området og sammenlikne med trekantens areal.
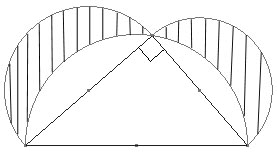
Ser vi litt nøye på figuren oppdager vi at hele figurens areal kan regnes ut på to ulike måter. Vi kan se på det som summen
av arealet til den største halvsirkelen og de skraverte områdene, eller vi kan se på det som summen av arealet til trekanten
og arealene til de to minste halvsirklene. Se følgende figurer:
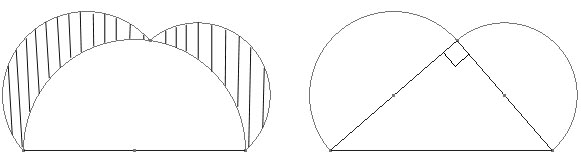
Altså:
(I) Arealet av største halvsirkel + Arealet av skraverte områder = Arealet av trekanten + Arealet
av minste halvsirkel + Arealet av mellomste halvsirkel
Velger å kalle de to katetene for henholdsvis a og b og hypotenusen for c (velger a <
b). Da får vi:
Arealet av den minste halvsirkelen = 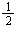 ·
p ·
·
p ·
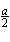 ·
· 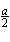 =
= 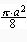
Arealet av den mellomste halvsirkelen = 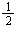 ·
p ·
·
p ·
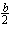 ·
· 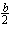 =
= 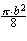
Arealet av den største halvsirkelen = 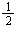 ·
p ·
·
p ·
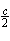 ·
· 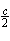 =
= 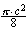
Arealet av trekanten = 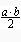
Setter inn i likning (I) over:
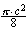 + Arealet av skraverte områder
=
+ Arealet av skraverte områder
= 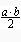 +
+ 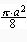 +
+ 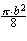
Arealet av skraverte områder = 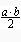 +
+ 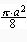 +
+ 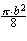 -
- 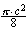 =
= 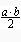 +
+ 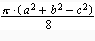 =
= 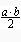 = Arealet av trekanten
= Arealet av trekanten
(Bruker her at 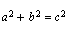 i følge Pytagoras
læresetning. Det vil si at
i følge Pytagoras
læresetning. Det vil si at 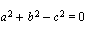 .)
.)
Konklusjonen er altså at arealet av de skraverte områdene er lik arealet av den rettvinklede trekanten.
Opprettet 2. mars 2001. Revidert 12. mars 2001.
Kjersti Melhus, HiS



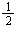 ·
p ·
·
p ·
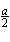 ·
· 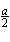 =
= 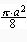
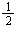 ·
p ·
·
p ·
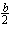 ·
· 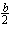 =
= 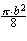
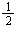 ·
p ·
·
p ·
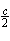 ·
· 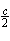 =
= 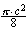
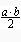
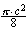 + Arealet av skraverte områder
=
+ Arealet av skraverte områder
= 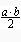 +
+ 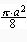 +
+ 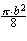
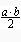 +
+ 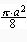 +
+ 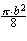 -
- 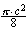 =
= 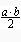 +
+ 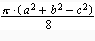 =
= 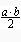 = Arealet av trekanten
= Arealet av trekanten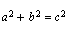 i følge Pytagoras
læresetning. Det vil si at
i følge Pytagoras
læresetning. Det vil si at 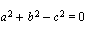 .)
.)