Oppgave 5.9.78 Det gylne snitt
a)
Obs: bredden er 1 (èn), ikke l
(liten L)
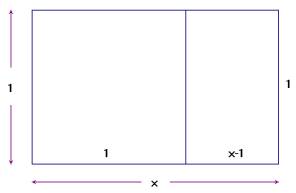
(forholdet
mellom lengde og bredde i det store rektanglet skal være lik forholdet mellom
lengde og bredde i det lille rektanglet.)
Multipliserer begge sidene
med x – 1, og får:
x (x – 1) = 1
x2 – x – 1 = 0 som var det
første vi skulle vise.
Dividerer begge sider med x,
og får:
som var det
vi skulle utlede.
b) Kjedebrøk :
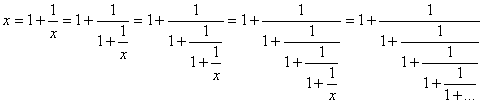
c) 1.
tilnærmelse:
1
2.
tilnærmelse:
3.
tilnærmelse:
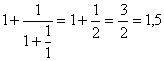
4.
tilnærmelse:
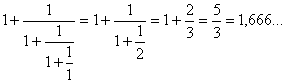
5.
tilnærmelse:
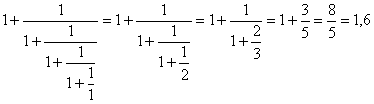
6. tilnærmelse:
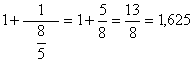
Ser et mønster som går igjen
i tilnærmelsene. Neste tilnærmelse får vi ved å la den forrige telleren være ny
nevner og la summen av den forrige teller og nevner være ny teller. (Kjenner du
igjen Fibonacci-tallene?)
|
n |
Teller |
Nevner |
Tilnærmelse nr n (teller /
nevner) |
|
1 |
|
|
1 |
|
2 |
2 |
1 |
2 |
|
3 |
3 |
2 |
1,5 |
|
4 |
5 |
3 |
1,666… |
|
5 |
8 |
5 |
1,6 |
|
6 |
13 |
8 |
1,625 |
|
7 |
21 |
13 |
1,6153846… |
|
8 |
34 |
21 |
1,6190476… |
|
9 |
55 |
34 |
1,617647… |
|
10 |
89 |
55 |
1,61818… |
|
11 |
144 |
89 |
1,617977528… |
|
12 |
233 |
144 |
1,6180555… |
|
13 |
377 |
233 |
1,61802575… |
|
14 |
610 |
377 |
1,618037135… |
|
15 |
987 |
610 |
1,618032786… |
|
16 |
1597 |
987 |
1,6180344478… |
d)
Tilnærmelsene fra c) ser ut til å konvergere mot
dette tallet.
e) Denne oppgaven lar seg ikke gjøre uten en kalkulator som ikke
prioriterer regneartene. Hvis du har en enkel kalkulator, så kan du sjekke om
den prioriterer regneartene ved f.eks. å trykke inn regnestykket 4 + 2 × 3 (i denne rekkefølgen). Får du svar 10,
prioriterer kalkulatoren regneartene (den utfører multiplikasjon og divisjon før
den utfører addisjon og subtraksjon, dersom ikke parenteser sier at den skal
gjøre noe annet). Dersom du får svaret 18, prioriterer den ikke regneartene
(den regner 4 + 2 = 6 og 6 × 3 = 18).
På en kalkulator uten prioritering av regningsartene,
får vi dersom vi begynner med 10, denne tallfølgen:
10
1,1 (
10 ¸ = + 1 = )
1,9090…
1,5238…
1,6562…
1,60377…
1,6235…
1,6159…
1,6188…
1,6177…
1,61815…
1,617989…
1,618051…
1,618027…
1,618036…
Tallene ser ut til å konvergere mot 
.
¸ = gir oss samme resultat
som 
.
|
Taster inn |
Får ut |
|
10
¸ = |
0,1 |
|
+
1 = |
1,1 |
|
¸ = |
1/1,1
= 0,90909… |
|
+
1 = |
1,90909… |
|
¸ = |
0,52381… |
|
+
1 = |
1,52381… |
Ser du likheten med kjedebrøken fra b)? Det femte
tallet i tallfølgen ovenfor er f. eks.
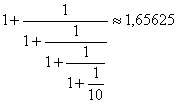
Opprettet
26.11.01
Høgskolen
i Stavanger