Oppgave
6.4.22
Oppgaven
lød:
A
og B er to punkter i planet. Konstruer det geometriske stedet for toppunktet
til en vinkel på 45° og hvis bein går gjennom A
og B.
Konstruksjon:
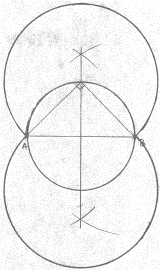
Forklaring:
Her
må vi bruke setninga om sentral- og periferivinkler (Thales setning). Hvis vi
tenker oss en periferivinkel på 45°, så vil den tilhørende
sentralvinkelen (som spenner over samme sirkelbue) være dobbelt så stor, altså
90°. Vi begynner med å finne toppunktet til
denne sentralvinkelen (som vil være sentrum i vår ønskede sirkelbue).
For
å finne toppunktet tar vi på nytt i bruk setninga om sentral- og
periferivinkler. Hvis vi tenker på den 90°'s vinkelen som en
periferivinkel, så vil tilhørende sentralvinkel være 180°. Det vil si at vinkelbeina til sentralvinkelen
vil være diameter i sirkelen.
Starter
med å konstruere midtnormalen til AB. Siden AB vil være korder i sirklene vi
vil fram til (vi får to stykker symmetrisk om AB), så vet vi at sentrene må
ligge på denne linja (midtnormalen til AB). Slår en sirkel med sentrum i midtpunktet
på AB og radius lik halve AB. Der sirkelen skjærer midtnormalen ligger sentrene
til de ønskede sirklene.
Slår
sirkelbuene med sentrum i skjæringspunktene vi nettopp fant og radius lik
avstanden fra disse og til A (eller B). Sirkelbuene utgjør det geometriske
stedet oppgaven spør etter (siden enhver periferivinkel med toppunkt på disse
buene og vinkelbein som går gjennom A og B vil være 45°).
OBS:
Legg merke til at det er en del av hver av de to sirklene som vi ikke tar med.
Det er nettopp disse sirkelbuene som de aktuelle sentral- og periferivinklene
"spenner over". En periferivinkel med toppunkt her vil ha tilhørende
sentralvinkel på 360° - 90° = 270° og vil derfor være 270° : 2 = 135° og ikke 45°. Det er derfor disse to sirkelbuene ikke tas
med.
Figur
som viser dette i det ene av de to symmetriske tilfellene:
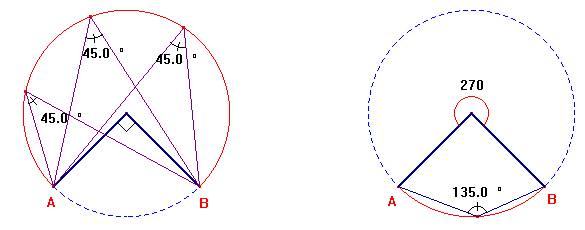
Opprettet 11.01.02
Høgskolen i Stavanger