Oppgave 6.4.23
Oppgaven lød:
A og B er to gitte punkter i planet med avstand 6 cm. Du
skal nå konstruere en trekant ABC, der ÐC = 30°
slik:
a)
Arealet av trekant ABC skal være 21 cm2. Konstruer trekanten.
b)
Arealet av trekant ABC skal være maksimalt. Konstruer ABC.
Løsningsforslag:
a) Dersom arealet
skal være 21 cm2, så må høyden i trekanten være 21 cm2 × 2 /
6 cm = 7 cm. C må altså ligge på en parallell linje 7 cm fra AB. (Legg merke
til at den parallelle linja i dette tilfellet kan konstrueres ved hjelp av kun én
rett vinkel og så to buer på 6 og 7 cm. Da bruker jeg det at i et rektangel er motstående
sider parallelle.)
Videre: hvis vi tenker på ÐC som
en periferivinkel med vinkelbein gjennom A og B, så vil den tilhørende
sentralvinkelen være 60°. Nå er jeg så heldig at jeg husker at i en likesidet er
alle vinklene 60°.
For å finne sentrum i sirkelbuen som vil gi meg det geometriske stedet for alle
toppunkt til 30°'s
vinkler med vinkelbein gjennom A og B, trenger jeg bare å konstruere en trekant
der alle sidene er like lange som AB. Det gjør jeg ved å slå to sirkelbuer med
radius AB og sentrum i henholdsvis A og B.
Når jeg har sentrum, kan jeg slå den ønskede sirkelbuen og se hvor den skjærer linja parallell med AB:
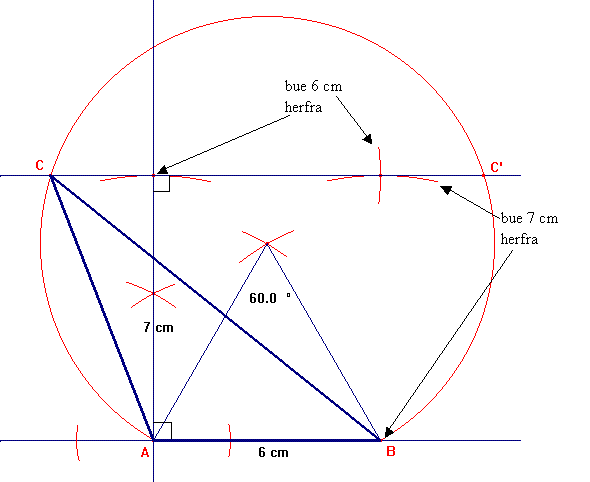
Vi får strengt tatt to
skjæringspunkt - på konstruksjonen kalt C og C' - men vi får bare beskjed om å
konstruere èn trekant, så vi kan velge hvilket vi vil bruke. Jeg valgte C. (I
tillegg får man to løsninger som ligger speilsymmetrisk om AB.)
b) Når
grunnlinja er gitt, så vil en trekant ha større areal jo større høyden er. Her
er det gitt at C skal ligge på sirkelbuen funnet i a). Størst mulig høyde får
vi dersom vi lar C ligge på midtnormalen til AB (da blir ABC en likebeint
trekant).
Konstruksjon (jeg lager en ny
figur her, så det ikke skal bli så mye rot, men du kan selvsagt konstruere i
figuren du har):
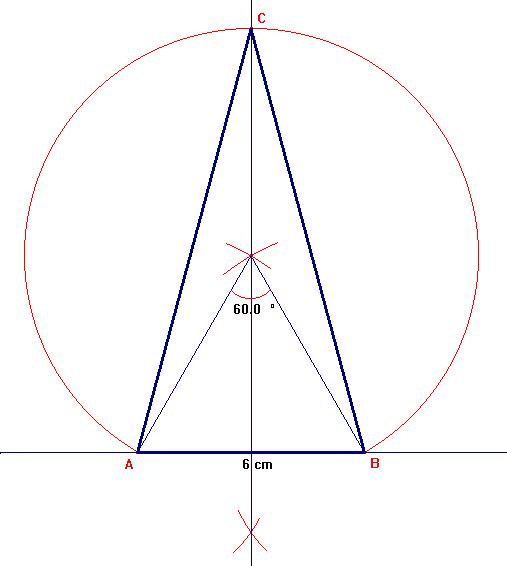
Opprettet, 16.01.02
Figurene redigert, 28.01.06
Universitetet i Stavanger