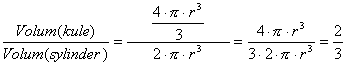Oppgave 6.9.74

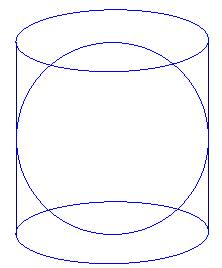
Figuren over viser en kule innskrevet i en sylinder. Det at den er innskrevet betyr at sylinderen er den minste sylinderen som rommer kula – dvs. at kula toucher

borti både veggen, bunnen og toppen av sylinderen.

Dette betyr at vi har følgende mål på sylinderen og kula:

Både kula og sylinderen har samme diameter. Dessuten er denne diameteren lik høyden i sylinderen (siden kula toucher bunnen og toppen).

La oss kalle si at radius til kula og sylinderen er r. Høyden h til sylinderen er da h = 2r.

Vi kan nå sette opp volum av sylinderen og av kula uttrykt ved r:

 
Sylinderen: p × r2 × h = p × r2 × 2r = 2 × p × r3  
Kula: 4 × p × r3 : 3 
 
Forholdet mellom kulas volum og sylinderens volum blir da:
 

 
hvilket vi skulle vise…
 
… dvs. i boka mi er det en trykkfeil – det blir man bedt om å vise forholdet er 1 : 3. Sunn fornuft sier at det er feil (volumet av kula må være mer enn en tredjedel 
av volumet av sylinderen). Utregningen vår slår fast at forholdet 1 : 3 er feil – det skal være 2 : 3. 
 
Det morsomme er at det samme forholdet finner vi også mellom overflatene til kula og sylinderen, men det overlater jeg til dere å vise.
 

Opprettet 16. april 2002
Kjersti Melhus, HiS