Fasit til problemoppgaver i kompendiet, s. 2-3

5. Frimerkeproblemet

1. Portotakster i Langtvekkistan. Undersøker systematisk hvilke portotakster jeg kan lage av 3- og 4-kroners frimerker:

Mulig portotakst	Eksempel på frimerkesammensetning
1	går ikke
2	går ikke
3	3
4	4
5	går ikke
6	3 + 3
7	3 + 4
8	4 + 4
9	3 + 3 + 3
10	3 + 3 + 4
11	3 + 4 + 4
12	4 + 4 + 4
13	3 + 3 + 3 + 4
…	…

Det ser ut til at alle portotakster fra og med 6 og oppover er mulig (i tillegg til 3 og 4).

2. Portotakster i Bortevekk (3- og 5-kroners frimerker):

Mulig portotakst	Eksempel på frimerkesammensetning
1	går ikke
2	går ikke
3	3
4	går ikke
5	5
6	3 + 3
7	går ikke
8	3 + 5
9	3 + 3 + 3
10	5 + 5
11	3 + 3 + 5
12	3 + 3 + 3 + 3
13	3 + 5 + 5
14	3 + 3 + 3 + 5
15	5 + 5 + 5
16	3 + 3 + 5 + 5
…	…

Det ser ut til at alle portotakster fra og med 8 og oppover er mulig (i tillegg til 3, 5 og 6).

3. Når du har klart å lage tre portotakster på rad, må du kunne lage alle større portotakster. Det er nemlig bare å sette et 3-kroners frimerke på en takst du allerede har.
Eksempel: Vi har 8 = 3 + 5

9 = 3 + 3 + 3 Her har vi nettopp tre på rad.

10 = 5 + 5

11 kan du lage ved å sette et 3-kroners frimerke på 8: 11 = 8 + 3 = 3 + 5 + 3

Osv.

4. 4- og 5-kroners:

Kan lage: 4, 5, 8, 9, 10, 12, 13, 14, 15, … alle videre portotakster går.

Her er det ikke nok med tre på rad. Siden det minste frimerke er 4, må du ha fire på rad!

3- og 7-kroners:

Kan lage: 3, 6, 7, 9, 10, 12, 13, 14, … alle videre portotakster går.

Her holder det med tre på rad, siden minste frimerke er 3.

5. Den siste portotaksten vi ikke kan dekke - undersøker:

Frimerker	Siste portotakst som ikke kan dekkes
3 og 4	5
3 og 5	7
4 og 5	11
3 og 7	11

Denne er like vanskelig for meg som den er for dere! (Og det selv om jeg har gjort oppgaven før!) Jeg har nå sittet og sett på dette i 10 minutter og tenkt så det knaker uten å se noe. Jeg har prøvd å legge sammen frimerkene og se hvordan summen er i forhold til tallene i høyre kolonne, men det ga meg ingenting. Nå ser jeg noe: 2 × 4 – 3 = 5

2 × 5 – 3 = 7

3 × 5 – 4 = 11 (denne skiller seg noe ut fra de andre)

2 × 7 – 3 = 11

Kan det være noe i dette?

Vi kan også sette opp: 3 × 3 – 4 = 5

4 × 3 – 5 = 7

4 × 4 – 5 = 11

6 × 3 – 7 = 11

Altså: det ser ut til at den første portotaksten som ikke går, alltid kan skrives som et tall ganger den ene frimerkeprisen minus den andre frimerkeprisen. Men hvordan hjelper det meg? Hvordan kan jeg vite hva jeg skal gange med?

Ha, der har jeg det! Glem det ovenfor. Se på produktet og summen av frimerkeprisene:

Frimerker	Produkt	Sum	Siste portotakst som ikke kan dekkes
3 og 4	12	7	5 = 12 – 7
3 og 5	15	8	7 = 15 – 8
4 og 5	20	9	11 = 20 – 9
3 og 7	21	10	11 = 21 – 10

For 3- og 10-kronersfrimerker vil den minste portotaksen vi ikke kan dekke være: 3 × 10 – (3 + 10) = 30 – 13 = 17 (hvis hypotesen min er riktig)

6. 4- og 6-kroners:

Kan lage: 4, 6, 8, 10, 12, 14, …

Kan selvsagt aldri lage "odde" portotakster, siden partall + partall alltid blir lik partall.

Det er kun når de to frimerkeprisene har største felles faktor lik 1 at vi kan lage alle takster over et visst beløp.

6. Myntproblemet

To sorter mynter: 5-kroner og 8-kroner.

Hvilke priser? (Forskjellen til frimerkeoppgaven, er at her kan du få penger igjen hvis du ikke har akkurat.)

Undersøker:

Mulig priser	Eksempel på handel
1	gir 2 × 8, får igjen 3 × 5
2	gir 2 × 5, får igjen 8
3	gir 8, får igjen 5
4	gir 4 × 5, får igjen 2 × 8
5	gir 5
6	gir 2 × 8, får igjen 2 × 5
7	gir 4 × 8, får igjen 5 × 5
8	gir 8
…	…

Jeg mistenker at alle (heltallige) priser går an.

Denne oppgaven kan man også utvide som den ovenfor.

Matematiske sett koker det ned til å finne heltallige løsninger til likningen: 5x + 8y = pris

Man kan vise (tema i Matematikk 3) at så lenge koeffisientene foran x og y har største felles faktor lik 1, så ha likningen løsning uansett pris.

7. Kaniner i bur

Velger en algebraisk løsning (denne oppgaven kan løses på flere nivåer – langt ned på barnetrinnet):

Anta Karin har x kaniner og y bur. Opplysningene gir oss følgende to likninger:

7y + 1 = x og 9(y – 1) = x

® 7y + 1 = 9y – 9 ® 2y = 10 ® y = 5

Karin har 5 bur!

x = 7y + 1 = 7 × 5 + 1 = 36

Karin har 36 kaniner! (Bør teste løsningen og se at den stemmer med opplysningene!)

8. Frosken Fred

Hver time kommer Fred seg opp en halv meter, men vi må passe på når han kommer til toppen. Det er lett å gi 20 timer til svar, men det blir feil. Det betyr jo at han har klatret en halv meter over brønnens slutt og så sklidd ned! Etter 18 timer befinner Fred seg 9 meter fra bunnen i brønnen. Den neste timen når han toppen, og han sklir ikke ned. Han bruker derfor 19 timer på å klarte opp av brønnen. (Eller i underkant av 19 timer siden han ikke bruker noe tid på å skli ned den siste timen.)

Denne oppgaven kan man fint løse ved tegning.

9. Et virvar av opplysninger

Langs brygga ligger fem båter av forskjellig type og farge. Båteierne har ulike hobbyer (i tillegg til båtlivet), de er fra hvert sitt land og er ikke like gamle. Bruk opplysningene under til å svare på spørsmålene.

LAND		Russland	Norge	Amerika	Sverige
BÅT	Havseiler	Knarr	Cabincruiser	Yngling	Soling
FARGE	Hvit	Brun	Gul	Blå	Rød
HOBBY	Bridge	Sjakk	Tennis	Hasard	Golf
ALDER	33	42	38	30

Ut fra de tomme feltene i tabellen ser vi at:

a) Det er eieren av havseileren som kommer fra Frankrike.

b) Det er svensken som er 28 år gammel.

Dette er forresten en typisk oppgave der du har fasiten når du har jobbet deg gjennom oppgaven. Forutsetningen er selvsagt at du har fulgt alle opplysningene til punkt og prikke. Det er ikke meningen at du skal gjette noe underveis.

En smart strategi er å gå gjennom lista av opplysninger til du treffer på en opplysning som du sikkert kan fylle inn i tabellen. (I denne oppgaven kan du ved første gjennomgang bruke opplysning nr. 9 og nr. 13.) Gå så gjennom lista gjentatte ganger helt til du har brukt alle opplysningene. Det er lurt å stryke ut opplysningene etter hvert som du har brukt dem.

Oppdatert 13.09.01:

For de som fortsatt syns dette er vanskelig, kan jeg fortelle i hvilken rekkefølge svarene faller på plass. Gå gjennom listen og sjekk at du er enig.

Her er rekkefølgen gitt ved nr. til påstandene (antar at jeg går gjennom listen fra topp til bunn og så starter på toppen igjen): 9, 13, 2, 11 (dette er et kritisk pkt som man må få til for å kunne gå videre!), 1, 4, 6, 7, 10, 3, 5, 8, 12 (kan plassere den brune båten, men må vente med å sette aldersopplysningen på plass), 14 (nå faller også aldersopplysningen fra 12 på plass)

10. Lett eller vanskelig? (Regnefeil rettet opp 09.11.01)

Skal finne ut hvor mange prosent det lille, grå kvadratet er av det store kvadratet.

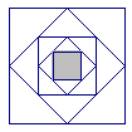
Løsning:

På figuren har vi fem kvadrater av ulik størrelse flettet inn i hverandre. Det største er akkurat dobbelt så stort som det neststørste. Det neststørste er dobbelt så stort som det nestneststørste osv. Størrelsen blir altså halvvert for hvert kvadrat innover. Det minste kvadrater er dermed av det største kvadratet.

(Her gjør jeg brøken 1/16 om til en brøk med 100 i nevneren. Husk at prosent betyr hundredel. Vi får at 1/16 er det samme som 6,25 hundredeler, dvs. 6,25 %.)

11. Hva blir de to neste tallene i tallrekkene? (det kan godt hende at det finnes flere ulike løsninger)

a) 3, 9, 15, 21, 27, 33, 39, … (differansen mellom tallene er 6)

b) 2, 3, 5, 8, 12, 17, 23, … (tallene øker med 1, 2, 3, 4, 5 osv)

c) 1, 3, 7, 13, 21, 30, 40, … (tallene øker med 2, 4, 6, 8, 10 osv)

d) 3, 4, 7, 11, 18, 29, 47, … (hvert tall er lik summen av de to forrige tallene)

e) 6, 24, 60, 120, 210, 336, 504, … (tredjedifferansen er 6. Denne var vrien – det kan godt være at det finnes flere løsninger.)

f) 5, 11, 25, 47, 77, 115, 161, … (andredifferansen er 8)

g) 3, 4, 6, 9, 13, 18, 24, … (tallene øker med 1, 2, 3, 4, 5 osv)

alternativ løsn:

3, 4, 6, 9, 13, 19, 28, … (9 = 3 + 6, 13 = 4 + 9, 19 = 6 + 13 osv)

h) 1, 2, 3, 6, 12, 24, 48, … (hvert tall er lik summen av alle de foregående tallene – når du ser bort fra de første tre tallene betyr det at hvert tall blir

det dobbelte av det forrige.)

i) 2, 5, 13, 35, 80, 152, 265, … (tredjedifferansen er 9)

Opprettet 07.11.01

Kjersti Melhus

Høgskolen i Stavanger